Specialization of Interpreters using Offline Narrowing-Driven Partial Evaluation.

Compilation by specialization of interpreters is a source to source program transformation. Narrowing-driven Partial Evaluation (NPE) is a powerful technique for the specialization of functional logic programs. Here it shows the stages of a novel pure offline partial evaluator developed in the functional logic language Curry which is able to specialize FlatCurry (the intermediate representation of Curry) programs. In particular, it describes the first experiments in the specialization of interpreters.  One method to formally describe the semantics of a programming language is by describing a procedure to evaluate statements that belong to the language to be defined, i.e., the description of an interpreter (Futamura, 1971). While interpreters are easier to write and maintain, they are inefficient. On the other hand the executable program of a compilation is more efficient, but is more expensive to implement. One way to get the best of both approaches is to implement a specialization of an interpreter, to automatically generate an efficient implementation (Thibault et al., 1998).

NPE (Albert and Vidal, 2002) is a powerful technique of specialization for the first order component of many functional languages like Haskell (Peyton-Jones, 2003) and functional logic as Curry (Hanus, 2006). At NPE, using a refinement of narrowing (Slagle, 1974) to perform symbolic computation, being needed narrowing (Antoy et al., 2000) the strategy that has better properties.

Pure offline partial evaluator (mixpo)

We call our offline partial evaluator as pure or 100% offline (mixpo) because all decisions about partial evaluation termination (well known like control issues) are taken before the proper specialization process. Thus, partial evaluation process is entirely directed by the annotations which were added during the BTA, i.e., the termination analysis is carried out at an early stage.

Binding Time Analysis. A BTA usually performs a static analysis to propagate the known (abstract) values throughout the entire program. In our case, the BTA computes a fixed point on the arguments of the program functions from the initial known values of a function call in order to specialize by considering only static (S) and dynamic (D) abstract values.

Size-change analysis lets to find out which function arguments into the function calls are increasing and hence they could cause infinite loops, for this, the analysis builds a set of size-change (multi) graphs that depict the arguments behavior. Roughly speaking, we use size-change graphs to approximate the changes in parameter sizes from one function call to another. In fact, we use the size-change graphs information to identify a particular form of quasi-termination (Dershowitz, 1987) called PE-termination in (Arroyo et al., 2007, p.60), this allows us to ensure quasi-terminating computations and as a consequence the finiteness of the partial evaluation process.

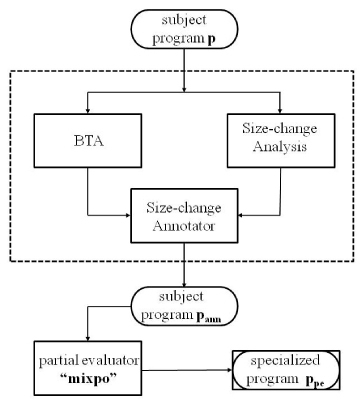
Figure 1. Outline offline partial evaluator (mixpo)

Figure 1 shows the complete scheme of our implementation, we can see that the process contained in the dotted box includes both simple BTA and size-change analysis, both processes take as input the program (p) to be specialized and deliver their results to the annotation process itself, that produces the annotated program (pann). Then, the partial evaluator (mixpo) receives pann and performs the proper partial evaluation process to produce a final specialized program ppe. We present an annotation procedure that is based originally on the quasi-termination analysis of (Arroyo et al., 2007, p.60), and it was improved at (Arroyo et al., 2007b, p.137). Moreover, since this quasi-termination analysis was originally introduced for TRSs, it was adapted to the flat language in this latter also.

Lets see a program specialization example:

Consider the fibonacci example for natural numbers shown below. In general we have calculated eight size-change graphs, but the size-change analysis yields as result three idempotent multigraphs shown in figure 2. Let us consider a call to the annotation stage with this program and the abstract initial value [D] for the argument ofmain definition. Our BTA returns the following division:

{main → (D); fib → (S); prod → (D,S); sum → (S, D)}

our annotation procedure returns the annotated program shown below as fibonacci after annotate.

Figure 2. Idempotent multigraphs for fibonacci

So far, we have described just the annotation stage. Taking the specialization stage, intuitively speaking, the source program before annotate shows that function fib can be fully evaluated, i.e., the program can be specialized just evaluating the function fib. If we use the annotated program (see below: fibonacci after annotate), we may see that you can fully unfold the both function as sum as fib because both are annotated with UNF. If you specialize the annotated program with our partial evaluator (mixpo) gets the program shown in the table “fibonacci after mixpo”, mixpo leaves the specialized program on “FlatCurry” language, however PAKCS (Hanus et al., 2004) is able to show this program in Curry. We can see, in fact, have been fully evaluated sum and fib. Likewise, the function prod has been partially evaluated.

The sources of the integrated application of the partial evaluator, can be found here. Once you download this file, you can uncompress it with:

  tar xvfz ver101018.tgz

In order to use the application modules, first you need to install the PAKCS (version 1.9.1) environment for Curry. Then, start PAKCS and load  the file Offpeval.curry as follows:

[Gustavo@localhost ver101018]$ pakcs
which: no rlwrap in (/usr/local/sicstus4.0.3/bin:/usr/lib/qt-3.3/bin:/usr/kerberos/bin:/usr/lib/ccache:/usr/local/bin:/usr/bin:/bin:/usr/X11R6/bin:/usr/local/sicstus4.0.3/bin/:

/usr/local/pakcs/bin/:/home/Gustavo/bin)
% restoring /usr/local/pakcs/curry2prolog/c2p.state...
  ______      __       _    _    ______   _______    
 |  __  |    /  \     | |  / /  |  ____| |  _____|   Portland Aachen Kiel
 | |  | |   / /\ \    | |_/ /   | |      | |_____    Curry System
 | |__| |  / /__\ \   |  _  |   | |      |_____  |  
 |  ____| / ______ \  | | \ \   | |____   _____| |   Version 1.9.1 (7)
 |_|     /_/      \_\ |_|  \_\  |______| |_______|   January 2009

Curry2Prolog(sicstus 4.0) Compiler Environment (Version of 13/01/09)
(RWTH Aachen, CAU Kiel, Portland State University)

Bug reports: mh@informatik.uni-kiel.de

Type ":h" for help

Prelude>:l OffPeval
Parsing 'OffPeval.curry'...
skipping FlatCurry.curry ...
skipping ChangeModuleName.curry ...
skipping FlatCurryGoodies.curry ...
skipping FlatCurryShow.curry ...
skipping FlexRigid.curry ...
skipping GNNTrees.curry ...
skipping OffPretty.curry ...
skipping Utils.curry ...
skipping btaFlat.curry ...
skipping General.curry ...
skipping RLNTpo.curry ...
skipping PostUnf.curry ...
skipping Prog2Flat.curry ...
skipping Resultants.curry ...
skipping ShowFlatCurry.curry ...
skipping dograph.curry ...
skipping gAnnotate.curry ...
skipping OffPeval.curry ...
OffPeval>

Now, you have available two commands:

• fannot "program" [initial division]: implements a quasi-termination analysis based on size-change graphs and a simple monovariant BTA in order to annotate the source program (returns "program_ann.curry") . It considers the UNF and MEM annotations. Furthermore, the vector for generalization (see this working draft sent to the GPCE 2011, for better explanation)
• mixpo "program_ann": it takes the annotated program and computes a partial evaluation of this program w.r.t. the first function definition in the program. It applies the pure offline specialization.

Continue with the specialization of interpreters

For instance, a typical session is as follows:

OffPeval> fannot "metainte/tesisexa/sinbasura/fib" [Dy]
--------------------------------------------------
      Full Annotator using a simple BTA & size-change graphs
--------------------------------------------------
Loading the program
Computing size-change graphs
**************************************************
Maximal Graph:

"fib"\1 |-| "fib"\1
1 -----  >  ----- 1

**************************************************


**************************************************
Maximal Graph:

"prod"\2 |-| "prod"\2
1 ------  >  ------ 1
2 ------  >= ------ 2

**************************************************


**************************************************
Maximal Graph:

"sum"\2 |-| "sum"\2
1 -----  >  ----- 1
2 -----  >= ----- 2

**************************************************



Computing binding-time division
Division incial: [[D],[S],[S,S],[S,S],[S],[S]]
div :[[D],[S],[S,S],[S,S],[S],[S]]
div :[[D],[S],[D,S],[S,S],[S],[S]]
div :[[D],[S],[D,S],[S,D],[S],[S]]
[("main",1,[D]),("fib",1,[S]),("prod",2,[D,S]),("sum",2,[S,D]),("UNF",1,[S]),("MEM",1,[S])]
Vector for Generalization
[("main",1,"UNF",[D]),("fib",1,"UNF",[S]),("prod",2,"MEM",[D,S]),("sum",2,"UNF",[S,D]),("UNF",1,"UNF",[S]),("MEM",1,"UNF",[S])]
Annotating program ...
Program succesfully annotated
Transforming annotated program to Curry...
module fib_ann(Nat(Z,S),GEN2,main,fib,prod,sum,UNF,MEM) where

import System

data Nat = Z | S Nat

GEN2 = BtD ("prod",2,[D,S])

main v1 = MEM (prod v1 (UNF (fib (S (S (S (S (S Z))))))))

fib eval rigid
fib Z = Z
fib (S Z) = S Z
fib (S (S v3)) = UNF (sum (UNF (fib (S v3))) (UNF (fib v3)))

prod eval rigid
prod Z v2 = Z
prod (S v3) v2 = UNF (sum v2 (MEM (prod v3 v2)))

sum eval rigid
sum Z v2 = v2
sum (S v3) v2 = S (UNF (sum v3 v2))

UNF v1 = v1

MEM v1 = v1


-- end of module fib_ann

Annotated program stored in <<metainte/tesisexa/sinbasura/fib_ann.curry>>
OffPeval> mixpo "metainte/tesisexa/sinbasura/fib_ann"
Offline Narrowing-Driven Partial Evaluator
(Version 0.1 of July 2009)
(Technical University of Valencia)

[(Comb FuncCall ("fib_ann","main") [(Var 0)])]
[("prod",2,[D,S])]

Main call: (main v0)


After postunfolding:
(main v0)=(prod_pe1 v0)
(prod_pe1 v1)=(Case v1 of
   (Z  -> (Z ))
   (S v6 -> (S (S (S (S (S (prod_pe1 v6)))))))
)



Writing original program into "metainte/tesisexa/sinbasura/fib_ann_pe.fcy"...

Specialization time (msecs): 50
OffPeval>
 

Continue with the specialization of interpreters

 Please report any bug or comment to garroyo (at) dsic.upv.es. 

Last update / Gustavo Arroyo